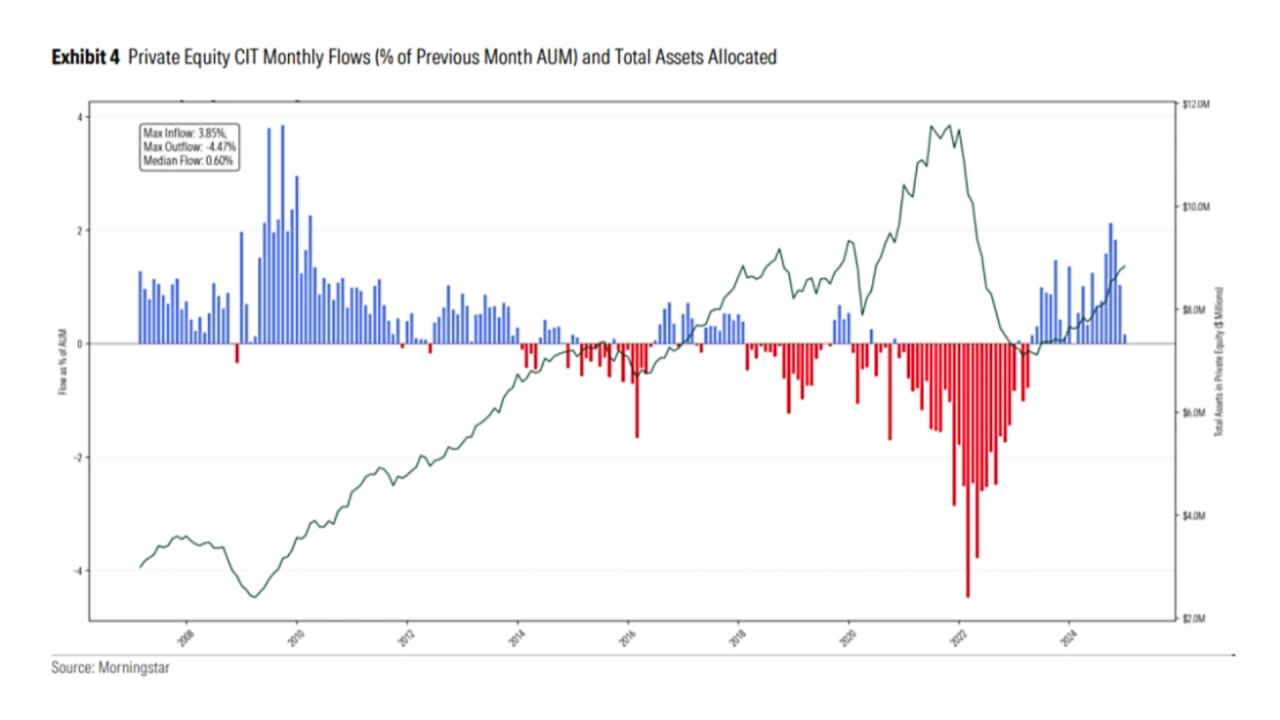
For clients who want minimal equity market risk in generating retirement income, the dominant options are building a bond ladder or purchasing a lifetime annuity.
The bond ladder is one of the most straightforward income strategies to give a client cash flow in each year of retirement. Just buy a series of bonds that will mature for the desired amount of spending in each year of retirement. Ideally, the payments are secured to an advanced age in case the retiree lives that long.
Unfortunately, if the retiree dies earlier than projected, there will be a lot of money left over that could have been spent but wasnt. But thats simply the risk of an unknown retirement time horizon.
In the case of a lifetime annuity, on the other hand, the time horizon is known, at least in the aggregate if not to the individual client because, with enough people, the mortality rate actually becomes highly predictable, even if it isnt known exactly which people will pass away from one year to the next.
Nonetheless, by operating on the assumption that some people will die each year, an annuity can pay out a portion of the funds that will eventually be left behind by those decedents.
This is important because it allows the immediate annuity to provide larger guaranteed payments for the group than any individual could generate on his/her own.
These excess payments are known as mortality credits, and they represent a unique aspect of lifetime annuities that doesnt exist with an individual bond ladder.
The advantage of mortality credits exists only by virtue of the fact that the other annuitants rather than the annuity owners heirs will benefit from any unused funds.
BOND LADDERS
Imagine for a moment that a 70-year-old retiree wishes to secure what he thinks will be a remaining 25-year retirement protecting against the risk of living to age 95 without taking any stock market risk. In that case, the retiree will simply buy a series of bonds that will provide the maximum possible level payments.
Assuming an average bond return of 3% (given current interest rates), the client could effectively amortize principal over a 25-year time horizon by spending $57.43 per year for each $1,000 in the portfolio. Like a mortgage amortization, the early years payments to the retiree will be primarily interest on the bonds and just a little bit of principal, and by the end almost all of each outbound payment will be principal and very little interest as the remaining principal balance approaches zero.
An example of the shifting composition of payments is shown at the top of the Amortizing Principal below.
Of course, retirees anticipating inflation may prefer to secure a rising stream of payments rather than level payments either by funding a bond ladder with TIPS and/or by structuring the planned withdrawals to start smaller (requiring less in principal liquidations in the early years) but rise over time.
The lower part of the chart shows the result if the client desires a payment stream that rises by 3% per year to keep up with inflation; the first payment is $41.20 and the last is $83.75. Again, the early payments are funded primarily by interest and the later ones increasingly from principal.
Of course, the drawback of this bond laddering approach is that your retiree doesnt truly know how long he is going to live. And even if the assumption of a 25-year retirement time horizon is highly conservative given his health and longevity expectations if he doesnt fear living beyond 95, that is there is also the risk that the retiree might live less than 25 years.
From his heirs financial perspective, that shorter life span might not be entirely bad news since it means there will be a nice inheritance. But it is unfortunate, at least in retrospect, for the retiree because it means he actually could have spent more during his lifetime, if only he had known in advance when his time would come.

POOLING FUNDS
At the most basic level, the value of using an immediate lifetime annuity to fund retirement income is that it solves for the challenge of the unknown time horizon and uncertain mortality by relying on the law of large numbers to create a predictable time horizon for an aggregated group of retirees.
For instance, imagine there are 25 retirees similar to the one above, each trying to solve for the same problem of spending down a portfolio of fixed assets over a maximum time horizon, and each taking the conservative spending amount necessary to fund the whole time period even though virtually none of them will actually live that long.
Instead of having each of the retirees fund their own portfolio, the group decides to pool its money, with the goal of having all of the participants receive their respective shares of principal and interest over time.
Whats significant about this arrangement is that, with a group structure, some of the people will not live until the 25-year time horizon. And with enough people (perhaps not 25, but certainly 25,000 or 250,000), its actually possible to predict with a high degree of accuracy exactly what percentage of the group will be alive from year to year.
This is a phenomenon known as the
Why does this matter? Because when its known, at least in the aggregate, what proportion of the partici pants will not live to any given year along that 25-year time horizon, it becomes safe to begin spending some of the expected leftover cash in advance.
In other words, when you know some people wont receive 25 years worth of payments, its safe to pay out more up front.
INCREASED PAYMENTS
For a simplified example of how this payment structure would work, imagine for a moment that, with our group of retirees, given the health of the group, the known mortality rate is that one person on average will pass away each year.
We dont know exactly when each individual will die. Yet with an average mortality rate of one person per year, we do know that while there are 25 people around to receive the first years payment, only 24 will still be alive to get the second, 23 will get the third, etc. until there is only one person alive by the 25th year to receive that last payment.
Given our earlier assumption of a 3% interest rate and this new mortality assumption, we can now calculate an anticipated annual level payment that would cover the time horizon (for those who will be alive) and spends down all the money.
And that payment is significantly higher than what an individual retiree could have achieved with the same $1,000, the same time horizon and the same assumed growth rate: $98.86 per year for each $1,000 contribution made by each individual, compared with only $57.43 with an individual bond ladder.
The whopping 70% difference in payments occurs because, as noted earlier, each individual has to assume a 25-year time horizon, while the aggregated group can reliably assume a shorter time horizon for some of the payments, recognizing that a portion of the group will pass away over time.
In turn, what this actually means is that some people will put in $1,000 and only receive a few $98.86 payments and, in fact, one person would receive only one payment while a few will put in the same $1,000 and receive 20 or more payments of $98.86 per year each, getting roughly twice what they paid in (or even more). Those who dont live very long will leave a large balance, which helps fund the payments for those who actually do live a long time.
In the real world, of course, the mortality rate for retirees is not a flat 4% per year; instead, the rate is lower for early retirees and then climbs higher for older retirees. Therefore, a real mortality curve would have a slightly smaller contribution of mortality credits in the early years and a slightly larger contribution in the later years, and the total payments for each $1,000 would be a little lower, because more people would survive longer on average.
Yet, conceptually, the notion of mortality credits remains the same; it allows for annuities to pay out significantly more to a pool of retirees than the equivalent funds invested in a bond ladder could pay to each of those retirees individually.
BEWARE PRINCIPAL GUARANTEES
One of the classic caveats to annuitization is the fact that assets, once annuitized, have no remainder value to leave to heirs. While some people will purchase an immediate annuity and live a long time receiving their original principal and then some in return others will make the purchase and then die unexpectedly, forfeiting what might have been a significant legacy bequest.
Yet the reality is that, with annuitization, the decision to give up any legacy bequest is what makes mortality credits possible in the first place. While theoretically any remaining unused funds could be set aside to be repaid at death and in point of fact, getting an immediate annuity with a refund guarantee of unrecovered principal does exactly that the act of doing so also converts an immediate annuity that pays principal, interest and mortality credits into one that simply pays principal and interest until principal is recovered.
If remaining funds cant be used to support the payments to others, then by definition there is no money to fund a mortality credit to increase everyones payments along the way.
In other words, obtaining a lifetime annuity that protects principal in the event of early death eliminates most of the actual benefit of purchasing the annuity in the first place, because keeping a legacy and accumulating mortality credits are the opposite sides of the same coin; if the remainder is kept for heirs, that amount cannot be used to fund higher payments for the group in the aggregate.
For instance, if the earlier example of an immediate annuity for 25 people had included a guarantee that the estate of anyone who died early would continue to receive payments until all principal was recovered, then all payments for the first 12 years would be guaranteed for all participants.
But as a result, only those who died in the last half of the 25-year time period would contribute to mortality credits at all. And by accumulating mortality credits for only half the time period, the payments themselves would be cut significantly from $98.86 per year to only $82.20 a year. While this is still an improvement over just amortizing principal and interest for 25 years, it cuts the benefit of mortality credits by nearly 40%. (See the Comparing Options chart below.)
The bottom line is this: For a given time horizon, annuities have the potential to produce greater payments than can be achieved from a fixed portfolio alone even if the annuity company invests the funds in the exact same manner due to the presence of mortality credits.
While lifetime immediate annuitization also presents the risk of losing out on any remaining principal as a legacy in the event of early death, it is the fact that the principal is at risk that makes mortality credits possible in the first place. By trying to limit the downside risk of early death with an annuity, retirees may forfeit a significant portion of the mortality credits they were trying to obtain by using the annuity in the first place.

Michael Kitces, CFP, a Financial Planning contributing writer, is a partner and director of research at Pinnacle Advisory Group in Columbia, Md., and publisher of the planning industry blog
Read more: